Elements of the triangle ::
about ::
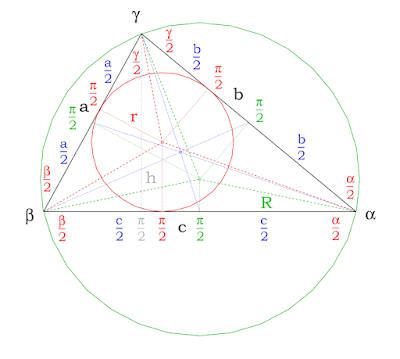
The interior angle bisectors of a triangle
Circumscribed circle - Wikipedia
Mollweide's formula - Wikipedia
...
def ::
\[\cases{a^2=b^2+c^2-2bc·Cos\ α\\ {}\\ b^2=c^2+a^2-2ca·Cos\ ß\\ {}\\ c^2=a^2+b^2-2ab·Cos\ \gamma}\]
\[2·p=P=a+b+c\]
\[\frac{abc}{4R}=pr=S=\sqrt{p\left({p-a}\right)\left({p-b}\right)\left({p-c}\right)}\]
\[2R^2\ Sin\ α\ Sin\ ß\ Sin\ \gamma=S=p^2\ Tan\ \frac α2\ Tan\ \frac ß2\ Tan\ \frac \gamma 2\]
\[\cases{h_a=\frac2a·S\\ {}\\ h_b=\frac2b·S\\ {}\\ h_c=\frac2c·S}\]
\[\frac1r=\frac1{h_a}+\frac1{h_b}+\frac1{h_c}\]
\[r^2=\frac{\left({p-a}\right)\left({p-b}\right)\left({p-c}\right)}p\]
\[2·R=\frac a{Sin\ α}=\frac b{Sin\ ß}=\frac a{Sin\ \gamma}\]
\[R=\frac{abc}{\sqrt{\left({a+b-c}\right)\left({b+c-a}\right)\left({c+a-b}\right)\left({a+b+c}\right)}}\]
\[S=\cases{\frac{a·h_a}2\\ {}\\ \frac{b·h_b}2\\ {}\\ \frac{c·h_c}2}=\cases{\frac{bc·Sin\ α}2\\ {}\\ \frac{ca·Sin\ ß}2\\ {}\\ \frac{ab·Sin\ \gamma}2}=\cases{\frac{a^2\ Sin\ ß\ Sin\ \gamma}{2\ Sin\ α}\\ {}\\ \frac{b^2\ Sin\ \gamma\ Sin\ α}{2\ Sin\ ß}\\ {}\\ \frac{c^2\ Sin\ α\ Sin\ ß}{2\ Sin\ \gamma}}\]
some x-ref formulas to verify the above figure and formulas ::
Some basics ::
The intersection of two lines ::
\[\cases{y=a_0·x+b_0\\ {}\\ y=a_1·x+b_1}\ →\ \left[{\Delta s=s_1-s_0}\right]\ →\]
\[\begin{array}{ccc}{from:\ y=ax+b\\ 0=x·\Delta a+\Delta b\\ thus:\\ x=-\ \frac{\Delta b}{\Delta a}=-\ \frac{b_1-b_0}{a_1-a_0}} & {\quad} & {from:\ \frac ya=x+\frac ba\\ y·\Delta\frac1a=0+\Delta\frac ba\\ thus:\\ y=\frac{\Delta\frac ba}{\Delta\frac 1a}=\frac{\frac{b_1}{a_1}-\frac{b_0}{a_0}}{\frac1{a_1}-\frac1{a_0}}=\frac{a_0b_1-a_1b_0}{a_0-a_1}}\end{array}\]
The intersection of an arbitrary line and the perpendicular line crossing it drawn through an arbitrary point ::
! note : the slope for the perpendicular line in the below tutor is
my notation : \(a_{\bot}=-\ \frac1a\) (about : Parallel and perpendicular symbol from Mathematica to $\LaTeX$ - Mathematica Stack Exchange)
the notation in the video tutor : \(m_{\bot}=-\ \frac1m\)
The intersection of two Circles ::
... write out general , analytical solution for the system :
\[\cases{\left(x-a_0\right)^2+\left(y-b_0\right)^2=R_0\\ {}\\ \left(x-a_1\right)^2+\left(y-b_1\right)^2=R_1}\]
etc. ...
[Eop]
No comments:
Post a Comment